Understanding Direct Current (DC) Circuit Theory: A Comprehensive Guide

DIRECT CURRENT (DC) CIRCUIT 

In direct current circuits, current flows in one direction only. Such current is said to be unidirectional. An electrical circuit is a symbolic representation showing all the components forming the circuit. 

DEFINITIONS 

Electric Current (I) 

Electric current is a measure of the rate of movement of charged particles along an electrical conductor. It is measured in ampere (A) using an ammeter. 

Electromotive Force (E)  

Electromotive force (emf) is the force which drives electrons round the circuit. It is measured in volts (V) using a voltmeter. 

Resistance (R) 

Resistance is the opposition offered to the flow of electric current in a circuit. It is measured in ohms (Ω) using an ohmmeter. 

Conductor 

A conductor is a material that readily allows the flow of electric current (charge) through it. Conductors have very low resistance to the flow of electric current. Examples are copper, aluminum, iron, silver etc.  

Electrolyte 

It is a substance whose aqueous solution conducts electric current. Examples are salts (sodium chloride), Potassium Carbonate acids (hydrochloric acid, tetraoxosulphate (v) acid and bases (copper oxide, sodium hydroxide).  

Insulator 

An insulator is a material that does not allow the flow of electric current through them. Insulators have high resistance to the flow of electric current. Examples are glass, plastics, porcelain, dry wood, polythene, ebonite, etc.  

Semiconductor 

A semiconductor is a material whose resistively lies between a good conductors and a good insulator. Examples are silicon, germanium, arsenic, indium, phosphorus etc.  

 

Sources of Energy 

Battery: A battery is the combination of two or more cells connected in series. 

Cell: A cell is a device that converts chemical energy into electrical energy. There are two basic sources of electrical energy.  

Primary Cells: They produce direct current and voltage and cannot be recharged when discharged. Examples are torchlight battery, watch battery etc.  

Secondary Cells: They produce direct current and voltage and can be recharged when discharged. Examples are lead acid accumulator, electric bell etc.  

 

Resistors 

A resistor is a device used to oppose/regulate the flow of electric current in a conductor. The magnitude/size of the resistor is referred to as resistance. 

TYPES OF RESISTORS 

(1) Carbon 

(2) Wire wound 

(3) Variable 

 

THE STANDARD COLOR CODE 

Resistor values are often indicated with color codes. The code is given by several bands. Together they specify the resistance value, the tolerance and sometimes the reliability or failure rate. 

Resistors color code is a system of identifying resistors by painting or coloring its bands. The resistance value, tolerance and wattage rating are generally printed on the resistors as numbers or letters. But when the resistors are small (e.g. 1/4W, 1/2W etc.), these specifications must be shown in some manner as the print would be small to read. Therefore, small resistors use color printed bands to indicate both their resistive value and their tolerance with the physical size of the resistor indicating its wattage rating. 

THE STANDARD COLOR CODE 

COLOR	BAND A 1ST NUMBER	BAND B 2ND NUMBER	BAND C NUMBER OF NOUGHT	BAND D TOLERANCE
BLACK	0	0	0	-
BROWN	1	1	1	1%
RED	2	2	2	2%
ORANGE	3	3	3	-
YELLOW	4	4	4	-
GREEN	5	5	5	-
BLUE	6	6	6	-
VIOLET	7	7	7	-
GREY	8	8	-	-
WHITE	9	9	-	-
SILVER	-	-	÷100	10%
NON	-	-	-	20%
PINK	-	-	-
GOLD	-	-	÷10	5%

Numerical Example

1. A resistor is coded, yellow, violet, red and gold. Determine the value of the resistor.

 

Solution

Yellow = 4, Violet = 7, R = 2, Gold = 5%

= 4700 + 5%

= 4700 × ⁵⁄₁₀₀

= 235Ω

Upper value = 4700 + 235 = 4935Ω  = 4.935KΩ

Lower value = 4700 – 235 = 4465Ω  = 4.465KΩ

Tolerance ranges from 4.465KΩ - 4.935kΩ

 

2. A resistor is coded green, blue, brown and silver. Determine the value of the resistor. 

 

Solution

Green = 5, Blue = 6, Brown = 1

Silver = 10%

560 ± 10%

560 × ¹⁰⁄100

= 56Ω 

Upper limit = 560 + 56 = 618Ω

                    = 0.616KΩ

Lower limit = 560 – 56 = 504Ω

                    = 0.504KΩ

Ranges from 504Ω - 616Ω.

 

3. A resistor marked with color bands red, violet, orange and gold has the value of? (NOVDEC. 2005 Objective Question 30)

 

Solution  

R = 2, Violet = 7, Orange = 3, Gold = 5% = 27000 ± 5%

 

= 27000 ×⁵⁄100 = 2,70k KΩ    

 

4. The resistance of 650 resistor of a tolerance of 10% ranges from? (SSCE May/June 2011 Objective Question 57)

 

Solution

Blue = 6, Green = 5, Brown = 0

= 650 ± 10%

650 ×¹⁰⁄100= 65 Ω   

Upper limit = 650 + 65 = 715Ω

Lower limit = 650 – 65 = 585Ω

Ranges from 585Ω - 715Ω  

Types of Resistors Connections 

1. Series connection  

2. Parallel connection  

3. Series-Parallel Connection  

Series Connection  

A resistor is said to be connected in series when the same current flows through each resistor. It implies that the resistors are connected on the same wire (conductor).  

The total (equivalent or effective) resistance is greater than the value of the highest individual resistance in the circuit.  

In series resistors, current is the same

I = I₁ + I₂ + I₃

Sum of Voltage drops equal the supply Voltage

V = V₁ +V₂ +V₃

V₁  =  IR₁,  V₂  =  IR₂,  V₃  =  IR₃

From Ohm’s Law

V  =  IR

V  =  IR₁  + IR₂  +  IR₃

IR =  IR₁  + IR₂  +  IR₃

Dividing through by I

R  =  R₁  +  R₂  +  R₃

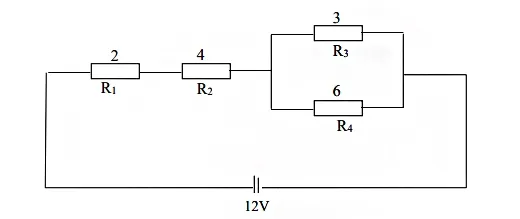
Example 

Calculate the total resistance in the circuit above.  

Solution

RT = R1 + R2 +R3 + R4

     = (2+1+3+4) Ω

     = 10 Ω 

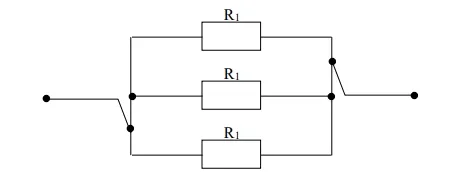
Parallel Connection  

A resistor is said to be connected in parallel with one another when the same voltage appears across each resistor.  

The total (equivalent or effective) resistance is less than the value of lowest individual resistance in the circuit. 

In parallel circuit, Voltage is the same

V  =  V₁  =  V ₂ =  V₃

Sum of currents through each component equal the supply current

I  =  I₁  +  I₂  +  I₃

 

From Ohm’s Law 

I  =  V/R

I₁ =  V/R₁,  I₂  =  V/R₂,  I₃  =  V/R₃

I  =  V/R₁  +  V/R₂  +  V/R₃

V/R  =  V/R₁  +  V/R₂  +  V/R₃

Multiplying through by 1/V 

 1/R   =   1/R₁   +   1/R₂   +   1/R₃

  

Example

Calculate the total resistance in the diagram above.

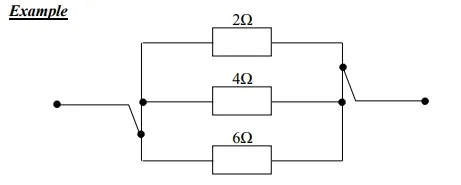
Solution

1/R_T   =   1/R₁   +   1/R₂   +   1/R₃

= 1/2 + 2/4 + 3/6

 = (6 + 3 + 1)/12

1/R_T  = 10/12

 R_T = 12/10 = 1.2 Ω

Further Reading: Parallel Circuits

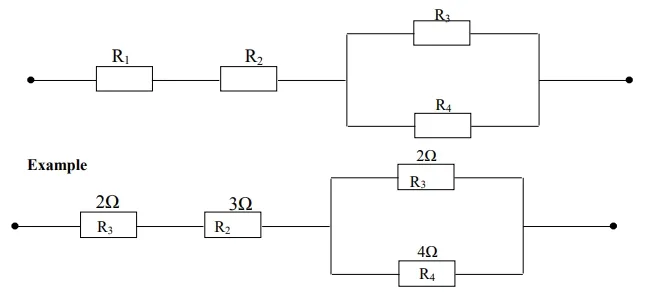
Series – Parallel Connection  

Resistors are said to be connected in series-parallel when the same current flows through the series resistors and the same voltage appears across the parallel resistor.  

Calculate the total resistance in the diagram above.  

Solution 

Finding the Total Resistance in Parallel

Given:

• $R_1 = 2 \, \Omega$
• $R_2=4\mathrm{\Omega }$

The formula for calculating the total resistance $R_T$ in a parallel circuit is:

$\frac{1}{R_T} = \frac{1}{R_1} + \frac{1}{R_2}$

Plugging in the values:

$\frac{1}{R_T} = \frac{1}{2} + \frac{1}{4}$

To add the fractions, find a common denominator:

$\frac{1}{R_T} = \frac{2}{4} + \frac{1}{4}$

$\frac{1}{R_T} = \frac{2 + 1}{4}$

$\frac{1}{R_T} = \frac{3}{4}$

Now, take the reciprocal to find $R_T$

$R_T = \frac{4}{3}$

So, the total resistance $R_T$ is:

$R_T = 1.33 \, \Omega$

Alternatively

Given:

• $R_3 = 2 \, \Omega$
  
• $R_4 = 4 \, \Omega$

The formula to find the equivalent resistance $R_p$ in a parallel circuit is:

$R_p = \frac{R_3 \times R_4}{R_3 + R_4}$

Plugging in the values:

$R_p = \frac{2 \times 4}{2 + 4}$

Calculating the product:

$R_p = \frac{8}{2 + 4}$

Now, add the resistances in the denominator:

$R_p = \frac{8}{6}$

Finally, simplify the fraction:

$R_p = \frac{8}{6} = 1.33 \, \Omega$

So, the equivalent resistance $R_p$ for the parallel connection of resistors 2 Ω and 4 Ω is approximately 1.33 Ω.

Then the circuit becomes  

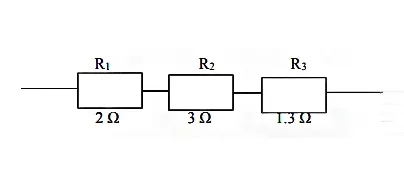
𝑅_𝑇 = 𝑅₁ + 𝑅₂ + 𝑅_𝑃

= 2 + 3 + 1.3 

= 6.3Ω 

Quantity of Electricity 

Quantity of electricity is defined as the quantity of electric current passing through a given point in a circuit in a length of time. It is measured in coulombs (c). 

Quantity of electricity = Current x time  

Q = It 

Q = Quantity of electricity (coulombs)  

I = Current (Ampere) 

T= Time interval (Seconds)  

Numerical Example 

1. The current flowing in a circuit is 2A. Calculate the quantity of electricity in the circuit in a time interval of 40 seconds.  

Solution 

Current (I) = 2A  

Time (t) = 40 seconds  

Quantity of electricity (Q) = ? 

Q= It  

   = 2 × 40 

   = 80c  

 

2. A current of 20mA flows for 2hrs through a circuit. Calculate the quantity of electricity passing through the circuit. 

Solution  

Current (I) = 20mA = 20X10-3 = 20/1000 = 0.02 

Time (t) = 2hs = 60s = 1m, 60m = 1hr, 120m = 2hrs, 

therefore 120X60 = 7200s 

Q = It  

   = 0.02 X7200 

  = 144c 

1. A current of 120mA flows for 3hrs through a circuit. Calculate the frequency of electricity passing through the circuit.  

2. The current flowing in a circuit is 6A. Calculate the time intervals in seconds if the quantity of electricity in the circuit is 240c.  

3. Calculate the current flowing in a circuit if the quantity of electricity in the circuit is 80c in a time interval of 40 seconds.  

OHM’S LAW 

Ohm’s law states that the current flowing through a metallic conductor is directly proportional to the potential difference (voltage) provided temperature is kept constant.  

 

I α V/R    →  I = KV/R

I = V/R

V = IR

 

NUMERICAL EXAMPLE 

A torch has 6V battery and a bulb of resistance of 12Ω. Calculate the current flowing through the bulb when the switch is closed.  

Solution 

Voltage (V) = 6V 

Resistance (R) = 12Ω Current (I) =?  

From ohm’s law, 

$I = \frac{V}{R}$

I  = 5/12

 

I  =  0.5A  

Power and Energy in DC Circuits

Electrical Power 

Power is defined as the rate of dissipating energy. The unit of power is the watts (W) and measured using a wattmeter. The power (P) consumed by a component in a DC circuit is calculated as the product of voltage and current:

$\text{Power} = \frac{\text{Energy}}{\text{Time}}$

P = I² R,           P = I V ,     

          $P = \frac{V^2}{R}$

$P = V \times I$

The energy (W) consumed over time (t) is given by:

$W = P \times t = V \times I \times t$

Where $W$ is measured in joules (J), $P$ in watts (W), $V$ in volts (V), $I$ in amperes (A), and $t$ in seconds (s).

Further Reading: Power in Electrical Circuits

Electrical Energy

Electrical energy is defined as the consumption of power in a length of time. It is measured in joules (J). 

E  =  Power × Time

E  =  I²Rt,   E  =  IVt    ,  E  = V²t/R

 

Numerical Example

(1) A cell of emf 5V is connected to a circuit of resistance 8Ω. Calculate; 

(a)  The current in the circuit 

(b)  The power consumed by the circuit 

(c)The energy consumed if the emf is connected for 22min 

Solution

Voltage (V) = 5V 

Resistance (R) = 8Ω

Time (t) = 22min 

(a) Current (I) = V/R = 5 /8     

                           

I = 0.625A

(b) P = IV = 0.625 X 5 

      P = 3.125 W 

(c) Energy (E) = 𝑃𝑜𝑤𝑒𝑟 × 𝑡𝑖𝑚𝑒  

E = I²Rt,  

But 1minute = 60seconds, 22minutes = (22x60)/1 = 1320s

                                                                    

     = 0.625 × 0.625 × 8 × 1320

     = 41255J

 

(2) A student leaves an electric iron on for a period of 8hours. If the iron has 2KW element, calculate the energy consumed in;

(a) Joules

(b) KJ

(c) KWh

Solution

Power (P) = 2KW =2000W

Time (t)    = 8H = 8 × 3600s = 28800s

Energy (E) =?

(a) E = Power × time

      E = 2000  × 28800

      E = 57600000J 

 

(b) E = 57600000/1000

      E = 57600KJ 

(c) E    = Power (KW) × time (h)

E = 2KW × 8h

      E = 16KWh

From the circuit above, calculate the; 

(a) Effective resistance in the circuit  

(b) Total current in the circuit  

(c)Current in the 6Ω resistor  

(d) Current in the 3Ω resistor

(e) Power in the 2Ω resistor  

(f) Energy consumed by 4Ω resistor  

If the circuit was on for 10 minutes  

Solution

Parallel 

Given:

• $R_3 = 3 \, \Omega$
• $R_4 = 6 \, \Omega$

The formula for the total resistance $R_p$ in parallel is:

$\frac{1}{R_p} = \frac{1}{R_3} + \frac{1}{R_4}$

Plugging in the values:

$\frac{1}{R_p} = \frac{1}{3} + \frac{1}{6}$

To add these fractions, find a common denominator:

$\frac{1}{R_p} = \frac{2}{6} + \frac{1}{6}$

$\frac{1}{R_p} = \frac{2 + 1}{6}$

$\frac{1}{R_p} = \frac{3}{6}$

Taking the reciprocal to find $R_p$:

$R_p = \frac{6}{3}$

So, the equivalent resistance $R_p$ is:

$R_p = 2 \, \Omega$

In Series connection 

Given:

• $R_1 = 2 \, \Omega$
• $R_2 = 4 \, \Omega$
• $R_p = 2 \, \Omega$

The formula for total resistance in series is:

$R_T = R_1 + R_2 + R_p$

Calculating:

$R_T = 2 + 4 + 2$

$R_T = 8 \, \Omega$

So, the total resistance $R_T$ is 8 Ω.

Total Current Calculation

To find the total current $I_T$, use Ohm's Law:

$I_T = \frac{V}{R_T}$

Given:

• Voltage $V = 12 \, \text{V}$

Plugging in the values:

$I_T = \frac{12}{8}$

$I_T=1.5\text{A }$

So, the total current $I_T$ in the circuit is 1.5 A.

 

 

(b) Current in the 6Ω resistor Using current divides rule

$I_{R4} = I_T \times \frac{R_3}{R_3 + R_4}$

Where:

• $I_T$ is the total current through the parallel combination.
• $R_3 = 3 \, \Omega$
• $R_4 = 6 \, \Omega$
• $I_T = 1.5 \, \text{A}$ (total current from the series circuit)

Plugging in the values:

$I_{R4} = 1.5 \times \frac{3}{3 + 6}$

Calculate the denominator:

$3 + 6 = 9$

So:

$I_{R4} = 1.5 \times \frac{3}{9}$

Simplify:

$I_{R4} = 1.5 \times \frac{1}{3}$

$I_{R4} = 0.5 \, \text{A}$

So, the current through $R_4$ is 0.5 A.

(c)    Current in the 3Ω resistor  

The formula to find the current through a resistor in a parallel circuit is:

$I_{R3} = I_T \times \frac{R_4}{R_3 + R_4}$

Where:

• $I_T$ is the total current through the parallel combination.
• $R_3 = 3 \, \Omega$
• $R_4 = 6 \, \Omega$
• $I_T = 1.5 \, \text{A}$ (total current from the series circuit)

Plugging in the values:

$I_{R3} = 1.5 \times \frac{6}{3 + 6}$

Calculate the denominator:

$3 + 6 = 9$

So:

$I_{R3} = 1.5 \times \frac{6}{9}$

Simplify:

$I_{R3} = 1.5 \times \frac{2}{3}$

$I_{R3} = 1 \, \text{A}$

So, the current through $R_3$ is 1 A

(d)    P_𝑅2 = (𝐼_𝑇)²  ×𝑅₂  

              = (1.5)² × 2

             = 2.5 × 2 = 4.5𝑊

 

(e)    Energy in 4Ω resistor in 10 minutes 

       10 minutes = 10 x 60 = 600s

       𝐸 = 𝐼²𝑅₄ × 𝑅₄ × 𝑡  

            = (1.5)² × 6 × 600

          = 2.25 × 4 × 600 

          = 900J

Resistivity and Conductivity 

Resistivity: Resistivity of a material is the ability of the material to oppose/regulate the amount of current flowing through the material. Resistivity is the reciprocal of conductivity. Low resistivity relates the materials having low opposition to the flow of current.  The resistance of a material depends on;

(a) The resistivity of the material (p) (Ωm) 

(b) The length of the material (l) (m)  

(c) The cross – sectional area of the material (𝑚2) 

 

Numerical Example 

(1)A copper wire has a length of 200m and a cross – sectional area of 0.2 × 10−6𝑚2. Calculate the;  

Resistance of the material if the resistivity of copper is 1.73 × 10−8Ω𝑚. 

Solution

Length (L) = 200m 

Area (a) = 0.2 × 10⁻⁶𝑚²

Resistivity (p) = 1.73 × 10⁻⁸Ω𝑚

Resistance (R) = ?

R   =   𝓅𝑙 /𝑎 

$\frac{(1.73 \times 10^{-8} \times 200)}{(0.2 \times 10^{-6})}$

Step-by-Step Calculation

1. Calculate the Numerator:

$1.73 \times 10^{-8} \times 200$

$= 1.73 \times 200 \times 10^{-8}$

$= 346 \times 10^{-8}$

$= 3.46 \times 10^{-6}$

2. Calculate the Denominator:

$0.2 \times 10^{-6}$

$= 2 \times 10^{-7}$

3. Divide the Numerator by the Denominator:

$\frac{3.46 \times 10^{-6}}{2 \times 10^{-7}}$

To simplify:

$\frac{3.46}{2} \times \frac{10^{-6}}{10^{-7}}$

$= 1.73 \times 10^{-6+7}$

$= 1.73 \times 10^1$

$=\mathrm{17.3 }$

 

     = 1730 × 10⁻² = 17.3Ω

 

(2) Calculate the resistance of 300m length of copper wire of diameter 1 mm whose resistivity is

1.73 × 10⁻⁸ Ωm

 

Solution

Length (l) = 300m

Resistivity ( = 1.73 × 10⁻⁸ Ωm  

Diameter (d) = 1mm = 1 × 10⁻³   

Area of conductor (a) = ?

$a = \frac{\pi d^2}{4}$

Where:

• $\pi \approx \mathrm{3.142 \; }$
• $d = 1 \times 10^{-3} \, \text{m}$

Step-by-Step Calculation

1. Square the Diameter:

$d^2 = (1 \times 10^{-3})^2$

$= 1 \times 10^{-6}$

2. Calculate the Numerator:

$\pi \times d^2 = 3.142 \times 1 \times 10^{-6}$

$= 3.142 \times 10^{-6}$

3. Divide by 4:

$a = \frac{3.142 \times 10^{-6}}{4}$

$=0.7855\times 10^{-\mathrm{6 }}$

$= 7.855 \times 10^{-7} \, \text{m}^2$

Result

The area $a$ is:

$a = 7.855 \times 10^{-7} \, \text{m}^2$

 

R   =   𝓅𝑙 /𝑎 

     = (1.73 × 10⁻⁸ x 300)/(  0.7855 x 10^-6) =   (51.9   x  10^-8)/(0.7855 x 10^-6 )    

     = 660.726 x 10^-2

     = 6.61Ω

 

Conductivity: Conductivity is the ability of a material to allow the free passing of electric current through it. The symbol for conductivity is (ϭ) sigma.

ϭ = 1/𝓅(Ωm)^-1

Conductance: Conductance is the reciprocal of resistance of a material. The symbol is G.G = 1/R Siemens (S)

 

Numerical Example

(1)  A copper wire has a resistance of 10Ω. Determine its conductance.

 

Solution

Resistance (R) = 10Ω

Conductance (G) =? 

  G =1/R = 1/10 = 0.15S

 

(2)  A copper wire has a conductance of 0.2 Siemens.  What is the resistance of the wire? 

 

Solution

Conductance (G) = 0.2S

Resistance (R) =? 

 R =1/G = 1/0.2 = 5Ω   

 

(3) A copper wire of length 50m has a conductance of 5 Siemens. Calculate the area of the conductor if the resistivity of copper is 0.0173Ωm. (Take 𝓅 = 0.0173µΩm)

Solution

Given Data

• Length of the wire ($L$) = 50 meters
• Conductance ($G$) = 5 Siemens
• Resistivity of copper ($\rho$) = 0.0173 µΩ·m

First, convert resistivity to Ω·m:

$\rho = 0.0173 \, \text{µΩ·m} = 0.0173 \times 10^{-6} \, \text{Ω·m}$

Steps to Calculate the Area

1. Calculate the Resistance ($R$) from Conductance:

$G = \frac{1}{R}$

Thus:

$R = \frac{1}{G}$

Plugging in the given conductance:

$R = \frac{1}{5}$

$R = 0.2 \, \text{Ω}$

2. Use the Formula for Resistance:

The formula for resistance is:

$R = \frac{\rho L}{A}$

Rearrange to solve for $A$:

$A = \frac{\rho L}{R}$

​

3. Plug in the Values:

$\rho =0.0173\times 10^{-6}$

$L = 50 \, \text{m}$

$R = 0.2 \, \text{Ω}$

Substitute these into the formula:

$A = \frac{0.0173 \times 10^{-6} \times 50}{0.2}$

4. Calculate:

$A = \frac{0.000000865}{0.2}$

$A = 0.000004325 \, \text{m}^2$

$A = 4.325 \times 10^{-6} \, \text{m}^2$

Result

The cross-sectional area $A$ of the copper wire is:

$A = 4.325 \times 10^{-6} \, \text{m}^2$

TEMPERATURE COEFFICIENT 

A temperature coefficient describes the relative change of a physical property that is associated with a given change in temperature.  

The resistance of most materials changes with temperature. In general, conductors increase their resistance as the temperature increases and insulators decrease their resistance with a temperature increase. 

Therefore, an increase in temperature has a bad effect upon the electrical properties of a material. Each material responds to temperature change in a different way, and constants have been calculated for each material (temperature coefficient of resistance ∝). 

 

Temperature coefficient values

Material	Temperature coefficient ( Ω/ Ω oС)
Silver	0.004
Copper	0.004
Aluminium	0.004
Brass	0.001
Iron	0.006
Carbon	-0.00048
Tin	0.0044

 

For a temperature increase from 0 ^oС

R_t = R_o (1 + ∝t) (Ω)

Where

R_t =  the resistance at the new temperature t ^oС

R_o = the resistance at  0 ^oС

∝  = the temperature coefficient for a particular material

For a temperature increase between two intermediate temperatures above 0 ^oС

R₁/R₂ = (1 + ∝t₁)/(1 + ∝t₂) 

Numerical Example

(1) The field winding of a D.C. motor has a resistance of 100Ω at 0 ^oС. Determine the resistance of the coil at 20 ^oС if the temperature coefficient is 0.004 Ω/ Ω ^oС.

 

Solution

Ro = 100Ω , t = 20 ^oС , ∝ =  0.004 Ω/ Ω ^oС

R_t = R_o (1 + ∝t)(Ω)

R_t = 100 Ω (1 + 0.004 Ω/ Ω ^oС × 20 ^oС)

Rt =  100 Ω (1 + 0.08)

Rt =  108Ω  

(2) The field winding of a generator has a resistance of 150Ω at an ambient temperature of 20 ^oС. After running for some time, the mean temperature of the generator rises to 45 ^oС. Calculate the resistance of the winding at the higher temperature if the temperature coefficient of resistance is 0.004 Ω/ Ω ^oС.

 

Solution

Given Data

• Initial resistance ($R_0$) = 150 Ω
• Initial temperature ($T_0$) = 20°C
• Final temperature ($T$) = 45°C
• Temperature coefficient of resistance ($\alpha$) = 0.004 Ω/Ω°C

Formula

The formula to calculate the resistance at the new temperature is:

$R_T=R_0(1+\alpha (T-T_0))$

Where:

• $R_T$ is the resistance at the higher temperature.
• $R_0$ is the initial resistance.
• $\alpha$ is the temperature coefficient of resistance.
• $\mathrm{T\; is\; the\; final\; temperature.}$
• $T_0$ is the initial temperature.

Calculation

1. Calculate the Change in Temperature:

$\Delta T = T - T_0$

$\Delta T = 45 - 20$

$\Delta T = 25 \, \text{°C}$

2. Substitute Values into the Formula:

$R_T = 150 \left(1 + 0.004 \times 25\right)$

3. Perform the Calculation:

$R_T = 150 \left(1 + 0.1\right)$

$R_T = 150 \times 1.1$

$R_T = 165 \, \text{Ω}$

Result

The resistance of the winding at the higher temperature of 45°C is:

$R_T = 165 \, \text{Ω}$

APPLICATIONS OF TEMPERATURE COEFFICIENT OF RESISTANCE 

(1) Positive Temperature Coefficient (PTC) Thermistors 

(2) Negative Temperature Coefficient (PTC) Thermistors 

(3) Heaters 

 

KIRCHHOFF’S LAWS 

The laws were proposed by a German physicist called Gustav Robert Kirchhoff (1824-1887) Junction/Node: A junction or node is point at which two or more conductors meet.  

 

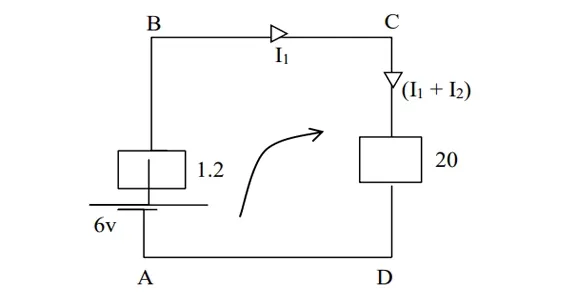
Kirchhoff’s First Law (Current Law)  

Kirchhoff’s first law states that the total current flowing towards a junction (node) in a circuit is equal to the total current flowing away from it.  

 

Implication of the First Law  

Current cannot accumulate within a circuit. 

Total current flowing towards the node N = 𝐼₃ + I₄

Total current flowing away from the node 

𝑁 =𝐼₁ +𝐼₂

 Therefore;  𝐼₁ + 𝐼₂ = 𝐼₃ + 𝐼₄

∑ 𝐼₁ +I₂   =   ∑ 𝐼₃ + 𝐼₄

(∑ 𝐼₁ + I₂) – (∑ 𝐼₃ + 𝐼₄) = 0

Algebraic sum of currents is zero.  

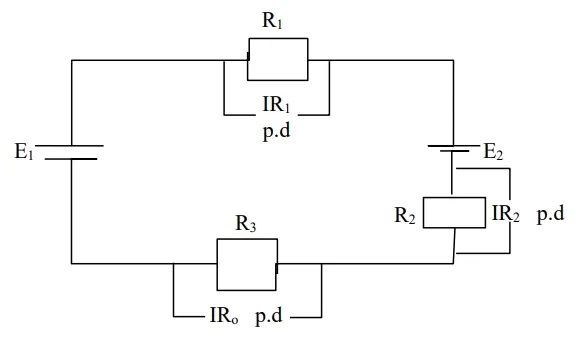
Kirchhoff’s Second Law (Voltage Law) 

Kirchhoff’s second law states that in any closed circuit, the algebraic sum of the potential drops and emf’s is zero. 

 

 

Implication of the   Second Law  

The sum of emfs + sum of pds = 0 

∑(𝑒𝑚𝑓𝑠) + ∑(𝑝𝑑𝑠) = 0  

𝐸₁ − 𝐸₂ = 𝐼𝑅₁ + 𝐼𝑅₂ + 𝐼𝑅₃

 

Numerical Example

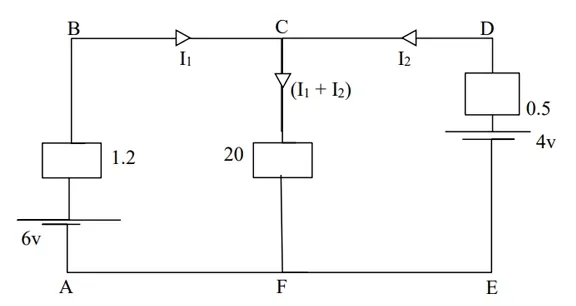
(1) Use Kirchhoff’s laws to calculate for; 

(a) The current through each battery 

(b)  The power dissipated in the 20Ω resistor 

(c)   The terminal voltage.  

6 = 1.2𝐼₁ + 20(𝐼₁ + 𝐼₂)

6 = 1.2𝐼₁ + 20𝐼₁ + 20𝐼₂

6 = 21.2𝐼₁ + 20𝐼₂           → (1)

Moving clockwise  

Consider loop ABDEA

6 − 4 = 1.2𝐼₁ − 0.5𝐼₂

2 = 1.2𝐼₁ − 0.5𝐼₂           → (1)

Matching both equation

6 = 21.2𝐼₁ + 20𝐼₂               → (1)

2 = 1.2𝐼₁ − 0.5𝐼₂           → (2)

Equation  (1) × 0.5 and Equation  (2) × 20  

3 = 10.6𝐼₁ + 10𝐼₂             → (3)

40 = 24𝐼₁ + 10𝐼₂             → (4)

Add equation  (3) and (4)

43   =   34.6𝐼₁

34.6      34.6

𝐼₁ = 1.243𝐴

𝑃𝑢𝑡 𝐼₁ = 1.243 𝑖𝑛𝑡𝑜 Equation  (1)

6 = 21.2𝐼₁ + 20𝐼₂       Equation  (1)

6 = 21.2(1.243) + 20𝐼₂

6 = 26.378 + 20𝐼₂

6 − 26.378 + 20𝐼₂

(−20.378)/20 = 20𝐼₂

 

𝐼₂ =-1.018A (It means the cell should be reversed) 

(a) 𝐼₁ + 𝐼₂ = (1.243) + (−1.018) = 10.225A

(b) Power dissipated in the 20Ω resistor 

𝑃 = 𝐼²𝑅

𝑃 = (𝐼₁ + 𝐼₂)² × 𝑅₂

0.225² × 20

  = 1.013W

(c)The terminal voltage 

𝑉𝑡 = 𝐸1 − 𝐼₁𝑅₁

= 6 − (1.243 × 1.2)

= 6 − (1.4916)

= 4.51𝑉

Alternatively 

Terminal voltage = (𝐼₁ + 𝐼₂) × 𝑅(1 + 2)

= 0.225 × 20

= 4.5𝑉

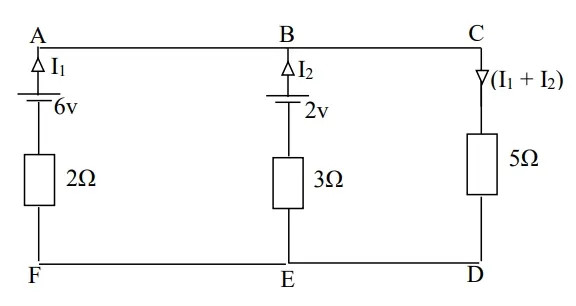
(2) Use Kirchhoff’s laws to calculate for; 

(a) The current flowing through each branch of the network 

(b) The power dissipated in the 5Ω resistor 

(c)The terminal voltage  

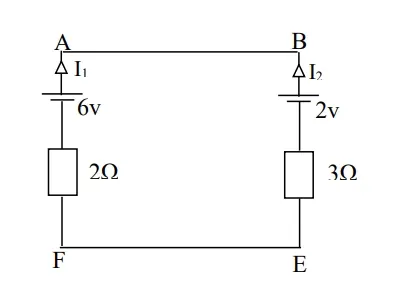
Consider loop ABEFA moving clockwise  

6 − 2 = 2𝐼₁ − 3𝐼₂

4 = 2𝐼₁ − 3𝐼₂ ………………………… (1)

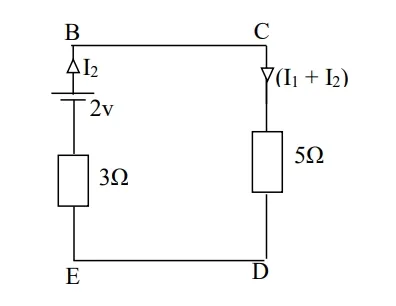
Consider loop BCDEB moving clockwise  

2 = 3𝐼₂ + 5(𝐼₁ + 𝐼₂)

2 = 3𝐼₂ + 5𝐼₁ + 5𝐼₂

2 = 8𝐼₂ + 5𝐼₁

2 = +5𝐼₁ + 8𝐼₂ ………………………… (2)

Matching equation (1) and (2) 

4 = 2𝐼₁ + 3𝐼₂  ………………………… (1)

2 = 5𝐼₁ + 8𝐼₂   ………………………… (2)

equation (1) × 8  

equation  (2) × 3  

32 = 216 + 24𝐼₂ ………………………… (3)

6 = 215 + 24𝐼₂   ………………………… (4)

equation (3) + (4)

38/31  = (31𝐼₁)/31

𝐼₁ = 1.226 𝐴

𝑃𝑢𝑡𝑡𝑖𝑛𝑔 𝐼 = 1.226 𝑖𝑛𝑡𝑜 equation  ( 2 )

2 = 5 𝐼₁ + 8𝐼₂

2 = 5(1.226) + 8𝐼₂

2 = 6.13 + 8𝐼₂

2 − 6.13 = 8𝐼2

−4.13 = 8𝐼₂

    8           8

𝐼₂ = −0.5163𝐴

𝐼₁ + 𝐼₂ = (1.226) + (−0.513)

= 0.7098A

 

(b) Power dissipated in 5resistor

𝑃 = 𝐼²𝑅

𝑃 = (𝐼₁ + 𝐼₂ )² × 5

𝑃 = 0.5038 × 5

𝑃 = 2.19𝑊

 

(c)The terminal voltage

= (𝐼₁ + 𝐼₂ × 𝑅(1 + 2))

= 0.7098 × 5

= 3.549𝑉

Alternatively

= 𝐸₂ − 𝐼₂𝑅₂

= 2 − (0.5163)  × 3

= 2 + 1.5489

= 3.5489V

 

Further Reading: Kirchhoff's Circuit Laws

Trial Test

1.      A p.d. of 5V is maintained across a resistance of 0.8Ω. Calculate the current flowing through the resistor.

 

2.      An electric heater has a rating of 2KW at 250V supply. Calculate the 

(a)   current drawn by the heater

(b)  resistance of the heating element

 

3.      Calculate the resistance of 100 metres of aluminium cable of 1.5mm2 cross-sectional area if the resistivity of aluminium is taken as 28.5  10^-9 Ωm.

 

4.      A coil of copper wire has a resistance 200Ω when its mean temperature is 0 ^oС. Calculate the resistance of the coil when its mean temperature is 80 ^oС.

 

5.      The field winding of a generator has a resistance of 10Ω at an ambient temperature of 20 ^oС. After running for some time the mean temperature of the generator rises to 33.4

^oС. Calculate the resistance of the winding at the higher temperature if the temperature coefficient of resistance is 0.004 Ω/ Ω ^oС.

 

6.      State Kirchhoff’s laws 

7.      Use Kirchhoff’s laws to calculate for 

(a) The current flowing through each branch of the network 

(b) The power dissipated in resistor. 

(c)The terminal voltage  

Applications of DC Circuits

DC circuits are widely used in various applications, including:

• Battery-Powered Devices: Many portable electronics, such as smartphones and laptops, operate on DC power supplied by batteries.
• Solar Power Systems: Solar panels generate DC electricity, which is used directly or converted to AC for broader applications.
• Automotive Systems: Vehicles use DC circuits for lighting, ignition, and control systems.

Further Reading: Applications of Direct Current

Conclusion

DC circuit theory is fundamental to understanding the behavior and operation of electrical circuits where current flows in a single direction. By mastering the concepts of voltage, current, resistance, and the rules governing series and parallel circuits, one can analyze and design DC electrical systems effectively.

Related Topics on Applied Electricity 

• Emission of Electrons and Thermionic Devices
• Data Communication 
• Digital Electronics
• Magnetic Field
• Electromagnetism
• Electric Field
• Direct Current Circuit Theory
• Applied Electricity Concise Notes for Senior High Schools (SHS 1, 2 & SHS 3)
• Careers in Applied Electricity
• Common Electrical Devices and Their Uses
• The Impact of Applied Electricity on Modern Technology