Digital Electronics Made Easy: Understanding Logic Gates, Circuits, and Design

DIGITAL ELECTRONICS

Digital electronics is the branch of electronics that deals with the study and application of digital signals to process information. Unlike analog electronics, which uses continuous signals, digital electronics employs discrete signals that represent data in binary form—0s and 1s. This binary system forms the foundation of digital technology, enabling the efficient processing and storage of data in a wide range of applications.

Key Takeaways

Binary System: Digital electronics uses the binary system, consisting of two states: 0 (off) and 1 (on). This simplicity allows for complex computations and data manipulations.

Precision and Accuracy: Digital signals provide high precision and accuracy in data processing, making them ideal for complex calculations and reliable communications.

Miniaturization: Digital electronics enables the creation of compact, efficient devices, leading to the proliferation of portable technology.

For a deeper understanding of the transition from analog to digital electronics, check out this article on the evolution of electronics.

Basic Concepts and Terminology

Understanding digital electronics requires familiarity with specific terminology and concepts. Here are some fundamental terms that are essential for grasping the intricacies of this field:

Digital Signals

Digital signals are electrical signals that represent data as discrete values. Unlike analog signals, which vary continuously, digital signals switch between distinct levels, commonly referred to as "high" and "low," representing binary digits (bits).

Binary System

The binary system is a base-2 numeral system that uses two symbols, typically 0 and 1, to represent data. This system is the backbone of digital electronics, allowing complex data to be encoded in a simple and efficient manner.

Bit and Byte

Bit: A bit is the smallest unit of data in digital electronics, representing a single binary value (0 or 1).
Byte: A byte consists of 8 bits and is commonly used as a unit of data storage.

Logic Levels

Logic levels refer to the specific voltage levels that represent binary values in a digital circuit. For example, a voltage close to 0V may represent a logic 0, while a higher voltage (e.g., 5V) represents a logic 1.

Boolean Algebra

Boolean algebra is a mathematical framework used to analyze and simplify digital circuits. It employs logical operations such as AND, OR, and NOT to manipulate binary values.

Truth Tables

Truth tables are used to illustrate the output of a digital circuit based on various combinations of input values. They are essential tools for designing and analyzing logic circuits.

Clock Signal

A clock signal is a periodic waveform that synchronizes the operations of digital circuits. It acts as a timing reference, ensuring that all components operate in harmony.

Flip-Flop

A flip-flop is a basic memory element in digital electronics, capable of storing a single bit of data. It is a building block for more complex memory structures.

ADC and DAC

ADC (Analog-to-Digital Converter): Converts analog signals into digital form.
DAC (Digital-to-Analog Converter): Converts digital signals back into analog form.

Integrated Circuits (ICs)

Integrated circuits are compact semiconductor devices that contain numerous interconnected electronic components, such as transistors and resistors. They are crucial for creating complex digital systems on a small scale. .

Fundamental Components of Digital Electronics

Digital electronics relies on a variety of components to perform its functions. These components form the basis of digital circuits and systems, enabling the processing, storage, and communication of data.

Transistors

Transistors are the fundamental building blocks of digital electronics. They act as electronic switches that control the flow of current, allowing digital circuits to perform logical operations. The most common types of transistors used in digital electronics are:

Bipolar Junction Transistor (BJT): Utilizes both electron and hole charge carriers.
Field-Effect Transistor (FET): Uses an electric field to control current flow, offering high input impedance.

Resistors

Resistors are passive components that limit the flow of current in a circuit. They are used to control voltage levels and ensure the proper functioning of digital circuits.

Capacitors

Capacitors store and release electrical energy, playing a critical role in timing and filtering applications within digital systems.

Diodes

Diodes are semiconductor devices that allow current to flow in one direction. They are used for signal rectification and voltage regulation in digital circuits.

Logic Gates

Logic gates are the basic building blocks of digital circuits. They perform logical operations on one or more binary inputs to produce a single binary output. Common logic gates include:

AND Gate: Outputs true only if all inputs are true.
OR Gate: Outputs true if at least one input is true.
NOT Gate: Inverts the input signal.
NAND Gate: Outputs false only if all inputs are true.
NOR Gate: Outputs true only if all inputs are false.
XOR Gate: Outputs true if the inputs are different.
XNOR Gate: Outputs true if the inputs are the same.

Flip-Flops and Latches

Flip-flops and latches are essential components for storing binary data. They are used in memory elements and sequential logic circuits.

Multiplexers and Demultiplexers

Multiplexer (MUX): Combines multiple input signals into a single output line based on control signals.
Demultiplexer (DEMUX): Distributes a single input signal to multiple output lines based on control signals.

Registers and Counters

Registers and counters are used to store and manipulate binary data in digital systems. Registers hold data temporarily, while counters are used for counting and sequencing operations.

Memory Devices

Memory devices, such as RAM and ROM, store data and instructions for digital systems. They are essential for the functioning of computers and other digital devices.

Comparison of Analogue and Digital Waveforms

The digital waveform has two quite definite states, either on or off, and changes between these two states very rapidly. An analogue waveform changes its value smoothly and progressively between two extremes.

In an analogue system, changes in component value due to ageing and temperature can affect the circuit’s performance. Digital systems are very much less susceptible to individual component changes.

Analogue circuitry is easily contaminated by noise particularly when signal levels are very small. Digital signals however, have very large amplitude and can be made relatively free of noise thereby achieving high quality of sound reproduction.

Logic Gates and Circuits

Logic Circuits

Logic circuits have been developed to deal with these digital two-state switching circuits. Information is expressed as binary numbers, that is, numbers which consist of ones and zeros. The low level is called logic 0 and the high-level logic 1. The information is processed according to rules built into circuits made up of signal units called logic gates.

Logic Gates

Logic gates are the heart of digital electronics, enabling complex computations and data manipulations. Understanding their functions and how they interact is crucial for designing effective digital systems.

Basic Logic Gates

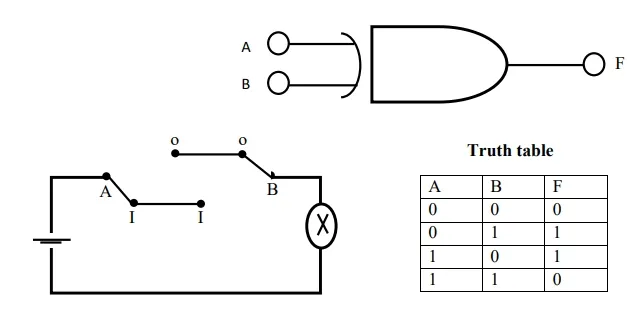
The AND Logic Gate

The AND gate outputs true (1) only if all its inputs are true (1). It performs the logical multiplication operation.

The signal lamp will only illuminate if both switch A and B are closed. Alternatively, the output F of the gate will only be at logic 1 if both input A and B are both at logic 1.

If the AND gate was operating a car handbrake warning lamp, it would only illuminate when both the handbrake and the ignition were on.

Switch Arrangements equivalent to AND logic

The lamp F only lights when both switches are closed.

Truth Table:

Input A	Input B	Output (A AND B)
0	0	0
0	1	0
1	0	0
1	1	1

The OR Logic Gate

The OR gate outputs true (1) if at least one of its inputs is true (1). It performs the logical addition operation.

The signal lamp will only illuminate if switch A or B or both switches are closed. We could also say that the output F will only be at logic 1 if input A or B or both inputs are at logic 1.

If the OR gate was operating an interior light in a motor car, it would illuminate when the nearside door was opened or the offside door was opened or when both doors are opened.

Switch Arrangements equivalent to OR logic

Truth Table:

Input A	Input B	Output (A OR B)
0	0	0
0	1	1
1	0	1
1	1	1

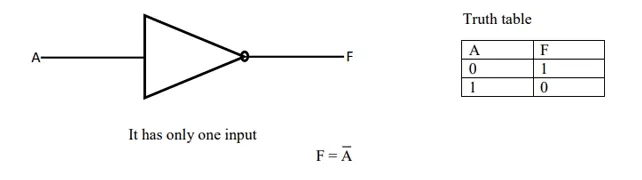
The NOT Logic Gate

The NOT gate is a single input gate which gives an output that is the opposite of the input. For this reason it is sometimes called an INVERTER, a NEGATOR or a SIGN CHANGER.

Truth Table:

Input	Output (NOT A)
0	1
1	0

The NAND Logic Gate

The NAND gate is a NOT gate and an AND gate combined to form a NOT –AND gate (NAND) gate. The output of the NAND gate is the opposite of the AND gate. It outputs false (0) only if all its inputs are true (1).

Truth Table:

Input A	Input B	Output (A NAND B)
0	0	1
0	1	1
1	0	1
1	1	0

The NOR Logic Gate

The NOR gate is a NOT gate and an OR gate combined to form a NOT-OR (NOR) gate. The output of the NOR gate is the opposite or inverse of the OR gate. It outputs true (1) only if all its inputs are false (0).

Truth Table:

Input A	Input B	Output (A NOR B)
0	0	1
0	1	0
1	0	0
1	1	0

The Exclusive -OR (XOR) Gate

Exclusive-OR gate with only two inputs will give logic 1 output only if input A or input B is at logic1, but not when both A and B are at logic 1.

Truth Table:

Input A	Input B	Output (A XOR B)
0	0	0
0	1	1
1	0	1
1	1	0

The XNOR Gate

The XNOR (Exclusive NOR) gate outputs true (1) if its inputs are the same.

Truth Table:

Input A	Input B	Output (A XNOR B)
0	0	1
0	1	0
1	0	0
1	1	1

Combining Logic Gates

Logic gates can be combined to create more complex circuits, such as adders, multiplexers, and decoders. These circuits form the building blocks of digital systems, enabling sophisticated data processing and control functions.

Example Circuit:

Here's a simple example of a combinational logic circuit using AND, OR, and NOT gates to achieve a specific output based on the given inputs.

Boolean Algebra and Logic Simplification

Boolean algebra is used to simplify logic expressions, reducing the number of gates required in a circuit. This simplification process is crucial for optimizing digital designs and improving their efficiency.

Boolean Laws and Theorems

Identity Law: $A + 0 = A,$ $A \cdot 1 = A$
Null Law: $A + 1 = 1$ , $A \cdot 0 = 0$
Idempotent Law: $A + A = A$ , $A \cdot A = A$
Inverse Law: $A + \overline{A} = 1$ , $A \cdot \overline{A} = 0$
Distributive Law: $A \cdot (B + C) = (A \cdot B) + (A \cdot C)$

Using these laws, complex logic expressions can be reduced to simpler forms, leading to more efficient circuit designs.

Karnaugh Maps

Karnaugh maps are graphical tools used to simplify logic expressions by visually identifying patterns and groups of terms. They provide a systematic approach to minimizing boolean functions, making it easier to design optimal circuits.

Buffers

A buffer has only one input and one output and its logical output is exactly the same as its input. Although the input and output voltage levels of buffer are identical, the currents present at the input and output can be very different.

TIMING DIAGRAM

Applications of Digital Electronics

Digital electronics is pervasive in today's world, with applications spanning numerous fields and industries. Its versatility and efficiency make it a cornerstone of modern technology.

Consumer Electronics

Digital electronics is integral to consumer electronics, powering devices such as:

Smartphones: Enabling communication, computing, and multimedia functions.
Televisions: Providing high-definition displays and interactive features.
Computers: Performing complex computations and data processing tasks.

Communication Systems

Digital electronics is the backbone of modern communication systems, facilitating:

Wireless Communication: Enabling mobile networks and internet connectivity.
Satellite Communication: Supporting global broadcasting and navigation systems.
Optical Communication: Allowing high-speed data transmission over fiber-optic cables.

Automotive Industry

Digital electronics is revolutionizing the automotive industry, enhancing:

Vehicle Control Systems: Implementing safety features and performance optimization.
Infotainment Systems: Providing navigation, entertainment, and connectivity options.
Autonomous Vehicles: Enabling self-driving capabilities through advanced sensors and algorithms.

Medical Devices

Digital electronics plays a vital role in healthcare, powering medical devices such as:

Diagnostic Equipment: Facilitating accurate imaging and analysis.
Monitoring Devices: Tracking vital signs and patient health metrics.
Wearable Technology: Offering personalized health monitoring and feedback.

Industrial Automation

Digital electronics drives industrial automation, improving:

Manufacturing Processes: Enhancing efficiency and precision in production lines.
Robotics: Enabling intelligent machines for various applications.
Control Systems: Optimizing operations and energy management.

Aerospace and Defense

Digital electronics is critical in aerospace and defense, supporting:

Navigation Systems: Providing accurate positioning and guidance.
Communication Networks: Ensuring secure and reliable data exchange.
Radar and Surveillance: Enhancing situational awareness and security.

Renewable Energy

Digital electronics contributes to renewable energy solutions by enabling:

Smart Grids: Optimizing energy distribution and consumption.
Solar Inverters: Converting solar energy into usable electricity.
Wind Turbine Control: Enhancing efficiency and performance.

Internet of Things (IoT)

The Internet of Things relies heavily on digital electronics to connect and control a vast array of devices, facilitating smart homes, cities, and industries.

Advantages of Digital Electronics

Digital electronics offers several advantages over analog electronics, making it the preferred choice for many applications.

Precision and Accuracy

Digital systems provide high precision and accuracy, allowing for reliable data processing and error-free communication.

Noise Immunity

Digital signals are less susceptible to noise and interference, ensuring consistent performance even in challenging environments.

Flexibility and Programmability

Digital circuits can be easily programmed and reconfigured, offering flexibility in design and application.

Miniaturization

Advancements in digital electronics have led to the miniaturization of components, enabling the creation of compact and portable devices.

Cost-Effectiveness

Mass production of digital components reduces costs, making digital technology accessible and affordable.

Scalability

Digital systems can be scaled to accommodate increased data processing needs, supporting the growth of complex applications.

Calculation Problems and Solutions

Here are some common calculation problems related to digital electronics, along with their solutions.

Problem 1: Logic Circuit Simplification

Given: Simplify the following logic expression:

$A \cdot (B + \overline{B}) + \overline{A} \cdot B$

Solution:

Using Boolean algebra, we have:

Apply the Complement Law: $B + \overline{B} = 1$
Simplify: $A \cdot 1 + \overline{A} \cdot B = A + \overline{A} \cdot B$
Apply the Absorption Law: $A + \overline{A} \cdot B = A + B$

Final Expression: $A + B$

Problem 2: Calculate the Output of a Logic Circuit

Given: A logic circuit with inputs $A = 1$ , $B = 0$ , $C = 1$ , and the circuit expression:

$(A \cdot B) + (\overline{A} \cdot C)$

Solution:

Calculate $A \cdot B$ : $1 \cdot 0 = 0$
Calculate $\overline{A}$ : $\overline{1} = 0$
Calculate $\overline{A} \cdot C$ $0 \cdot 1 = 0$
Calculate the final output: $0 + 0 = 0$

Output: 0

Problem 3: Find the Equivalent Resistance in a Digital Circuit

Given: A digital circuit with resistors $R_1 = 10 \Omega$ , $R_{2} = 20 Ω, and$ $R_3 = 30 \Omega$ connected in series.

Solution:

The equivalent resistance ( $R_{\text{eq}}$ ) in a series circuit is the sum of the individual resistances:

$R_{\text{eq}} = R_1 + R_2 + R_3$

$R_{\text{eq}} = 10 \Omega + 20 \Omega + 30 \Omega$

$R_{\text{eq}} = 60 \Omega$

Equivalent Resistance: $60 \Omega$

Problem 4: Calculate the Capacitance in a Digital Circuit

Given: A digital circuit with capacitors $C_{1} = 10 μ F,$ $C_{2} = 20 μ F , and$ $C_3 = 30 \mu F$ connected in parallel.

Solution:

The equivalent capacitance ( $C_{\text{eq}}$ ) in a parallel circuit is the sum of the individual capacitances:

$C_{\text{eq}} = C_1 + C_2 + C_3$

$C_{\text{eq}} = 10 \mu F + 20 \mu F + 30 \mu F$

$C_{\text{eq}} = 60 \mu F$

Equivalent Capacitance: $60 \mu F$

Problem 5: Calculate the Current in a Digital Circuit

Given: A digital circuit with a voltage source ( $V$ ) of 12V and a resistor ( $R$ ) of 4Ω.

Solution:

Using Ohm's Law ( $I = \frac{V}{R}$ ):

$I = \frac{12V}{4\Omega}$

$I = 3A$

Current: 3A

Future Trends in Digital Electronics

The field of digital electronics is continuously evolving, with several emerging trends shaping its future:

Artificial Intelligence and Machine Learning

Digital electronics is driving advancements in artificial intelligence (AI) and machine learning, enabling intelligent systems to process vast amounts of data and make informed decisions.

Quantum Computing

Quantum computing promises to revolutionize digital electronics by leveraging quantum mechanics to perform computations at unprecedented speeds and scales.

Internet of Things (IoT)

The proliferation of IoT devices is transforming industries, with digital electronics enabling seamless connectivity and data exchange between devices.

5G and Beyond

The rollout of 5G networks is set to enhance digital communication, offering faster speeds and more reliable connections for digital devices.

Wearable Technology

Wearable devices are becoming more sophisticated, with digital electronics enabling advanced health monitoring and personalized experiences.

Renewable Energy Integration

Digital electronics is playing a crucial role in integrating renewable energy sources into the grid, optimizing energy management and consumption.

Edge Computing

Edge computing is bringing data processing closer to the source, reducing latency and improving efficiency in digital systems.

Conclusion

Digital electronics is a dynamic and rapidly advancing field, underpinning the technological advancements that shape our world. From consumer electronics to industrial automation, its applications are vast and varied, offering endless possibilities for innovation and growth. By understanding the principles, components, and applications of digital electronics, we can better appreciate its impact on our lives and the future of technology.

Additional Resources

For further reading and exploration, consider the following resources:

Books:
- Digital Design and Computer Architecture by David Harris and Sarah Harris
- Fundamentals of Digital Electronics by Dhanasekharan Natarajan
Online Courses:
- Coursera: Digital Electronics
- edX: Digital Circuits
Websites:
- Electronics Tutorials: Digital Electronics
- All About Circuits: Digital

Emission of Electrons and Thermionic Devices
Data Communication
Digital Electronics
Magnetic Field
Electromagnetism
Electric Field
Direct Current Circuit Theory
Applied Electricity Concise Notes for Senior High Schools (SHS 1, 2 & SHS 3)
Careers in Applied Electricity
Common Electrical Devices and Their Uses
The Impact of Applied Electricity on Modern Technology

Digital Electronics Made Easy: Understanding Logic Gates, Circuits, and Design